N皇后问题解法三
编者:16计外1班 阿沐 指导老师:李老师
1、算法设计
递归算法:
相比于回溯算法,更方便地是用递归控制方式实现,用这种方式也可以解决任意的n皇后问题,算法思想和解法一二相同,用深度优先搜索,并在不满足的约束条件的情况下及时回溯。
设计技巧:
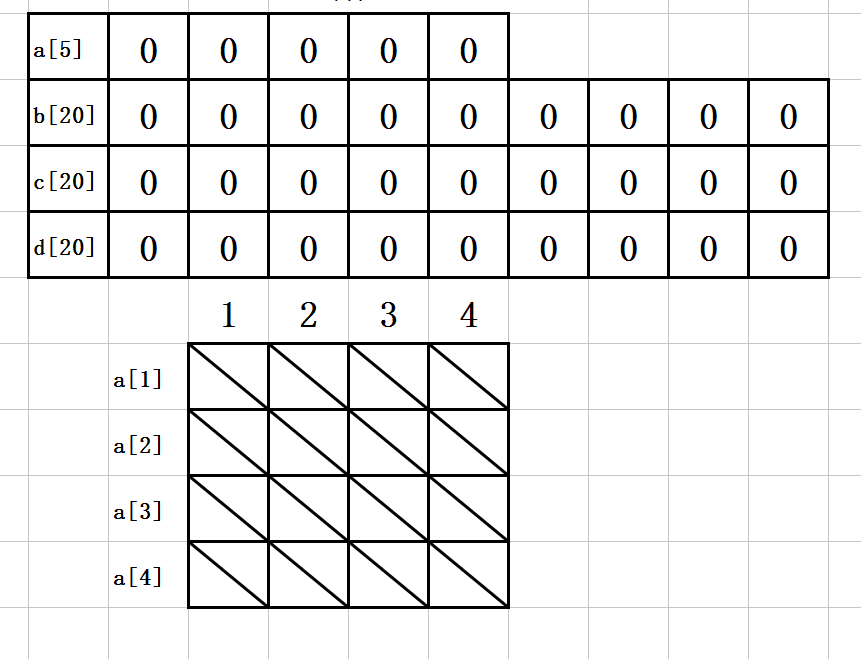
用4个数组记录信息:
a数组记录解的正确值;
b数组记录n个列;
c数组记录2n-1个主对角线的占用情况(1为占用,0为未占用);
d数组记录2n-1个负对角线的占用情况(1为占用,0为未占用);
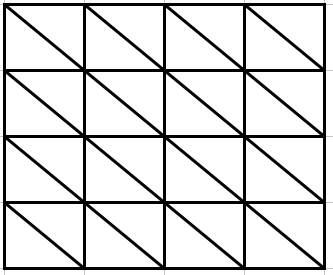
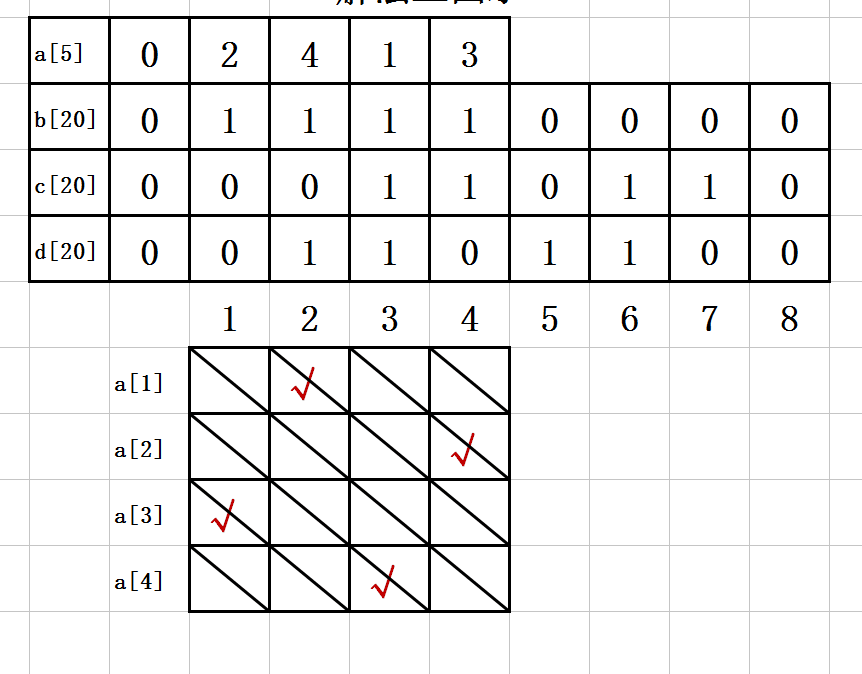
依旧以4阶棋盘为例:
共有2n-1=7个主对角线和7个负对角线。
用i,j分别表示皇后所在的行列(或者说i号皇后在j列),同一主对角线上的行列下标的差一样,若用表达式i-j编号,则范围为-n+1-->n-1,所以表达式i-j+n对主对角线编号,范围就是1-->2n-1。同样的,负对角线上行列下标的和一样,用表达式i+j编号,则范围为2-->2n。
2、代码实现(Java)
package gxr;
import java.util.Scanner;
public class QueenThree {
static int[] a=new int[20];//记录最终结果数组
static int[] b=new int[20];//记录棋盘的n个列
static int[] c=new int[40];//记录2n-1个主对角线的占用情况
static int[] d=new int[40];//记录2n-1个负对角线的占用情况
static int n;
static int t;//记录解的个数
static int i;
int j;
static int k;
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
System.out.println("请输入皇后个数:");
n=sc.nextInt();
for(i=1;i<=n;i++)//初始化数组
{
b[i]=0;
c[i]=0;c[n+i]=0;
d[i]=0;d[n+i]=0;
}
start(1);
}
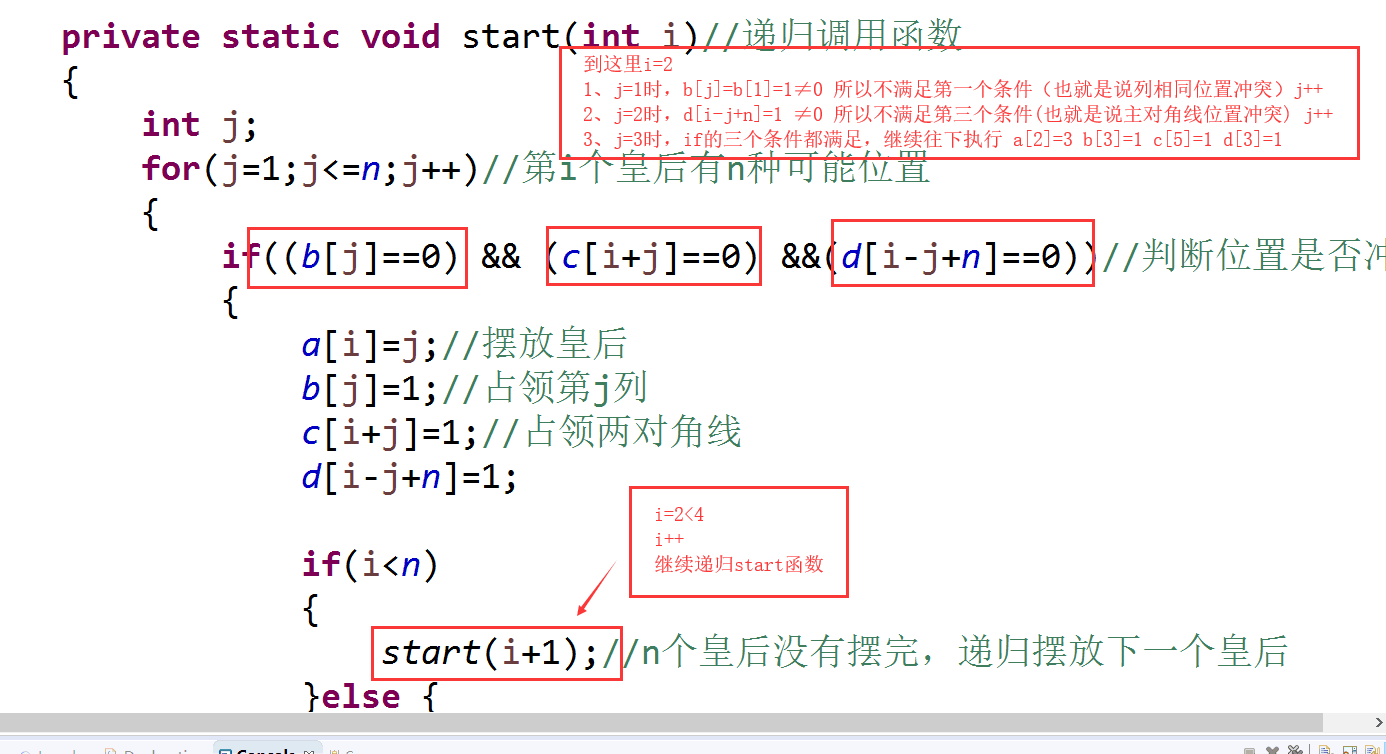
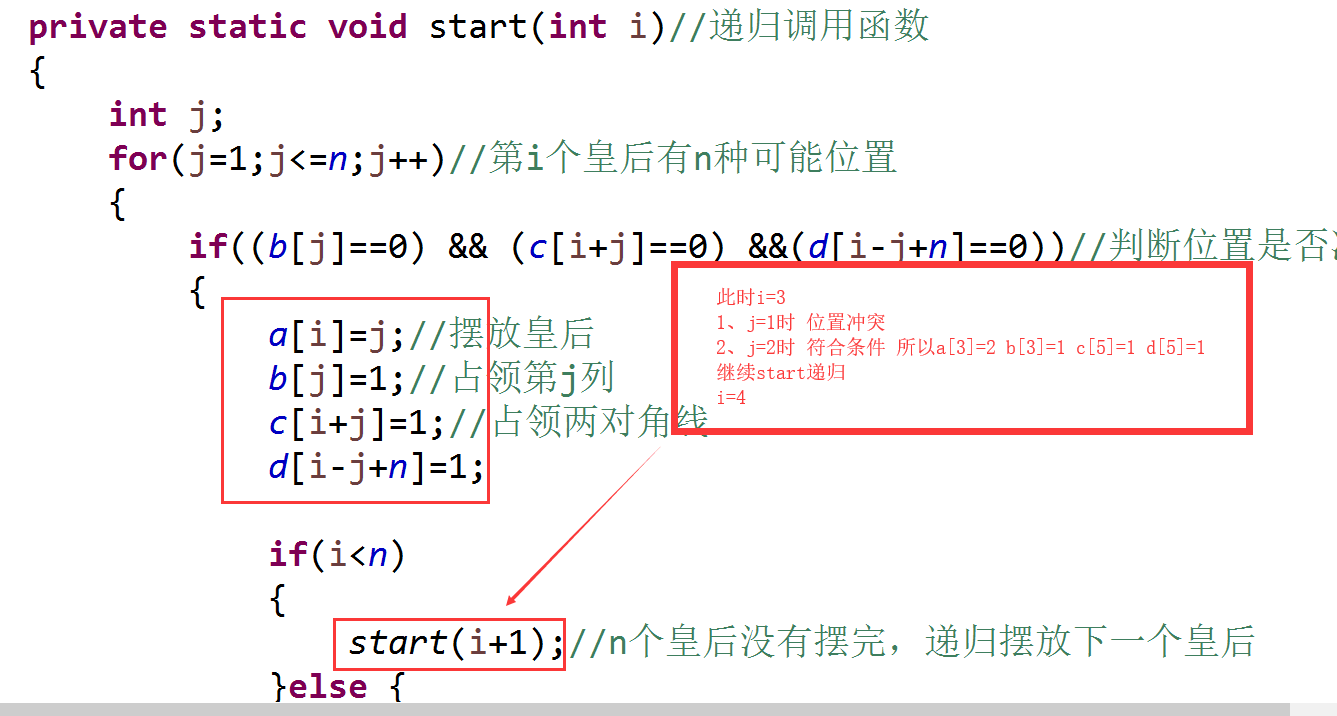
private static void start(int i)//递归调用函数
{
int j;
for(j=1;j<=n;j++)//第i个皇后有n种可能位置
{
if((b[j]==0) && (c[i+j]==0) &&(d[i-j+n]==0))//判断位置是否冲突
{
a[i]=j;//摆放皇后
b[j]=1;//占领第j列
c[i+j]=1;//占领两对角线
d[i-j+n]=1;
if(i<n)
{
start(i+1);//n个皇后没有摆完,递归摆放下一个皇后
}else {
output();//到这里就表示已经找到了一组满足约束的解
}
b[j]=0;
c[i+j]=0;
d[i-j+n]=0;
}
}
}
private static void output()//输出解
{
t++;
System.out.print("第"+t+"组解为:");
for(k=1;k<=n;k++)
{
System.out.print(a[k]+" ");
}
System.out.println();
}
}
3、推演过程
1. 初始图如下:
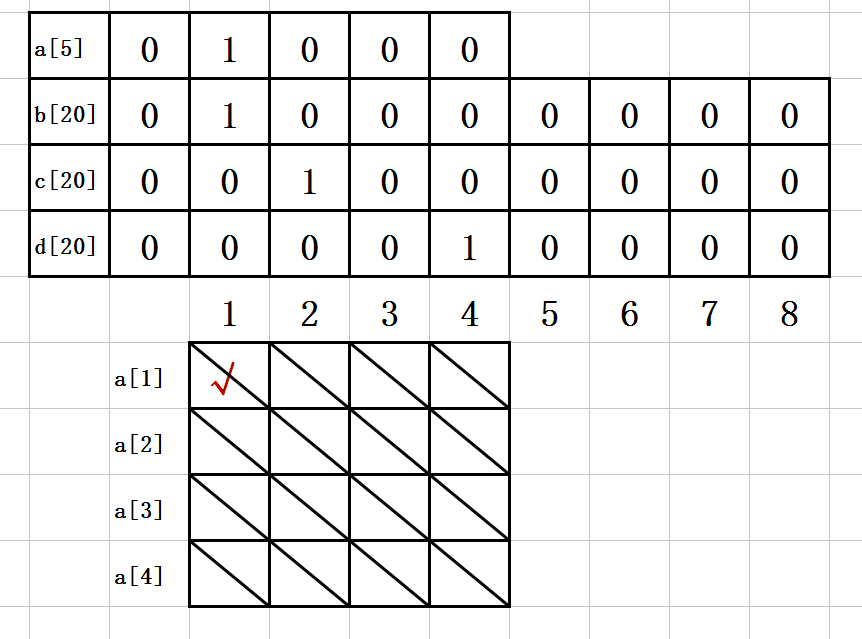
2. 第一步:
a[1]=1;
b[1]=1;
c[2]=1;
d[4]=1;
如图示:
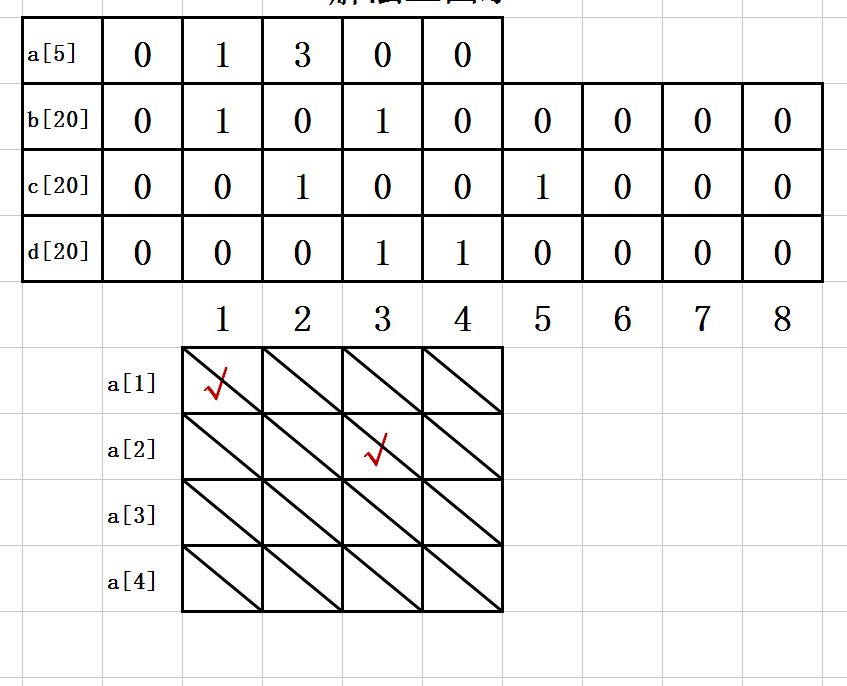
3. 第二步:
a[1]=1;
b[1]=1;
c[2]=1;
d[4]=1;
a[2]=3;
b[3]=1;
c[5]=1;
d[3]=1;
如图示:
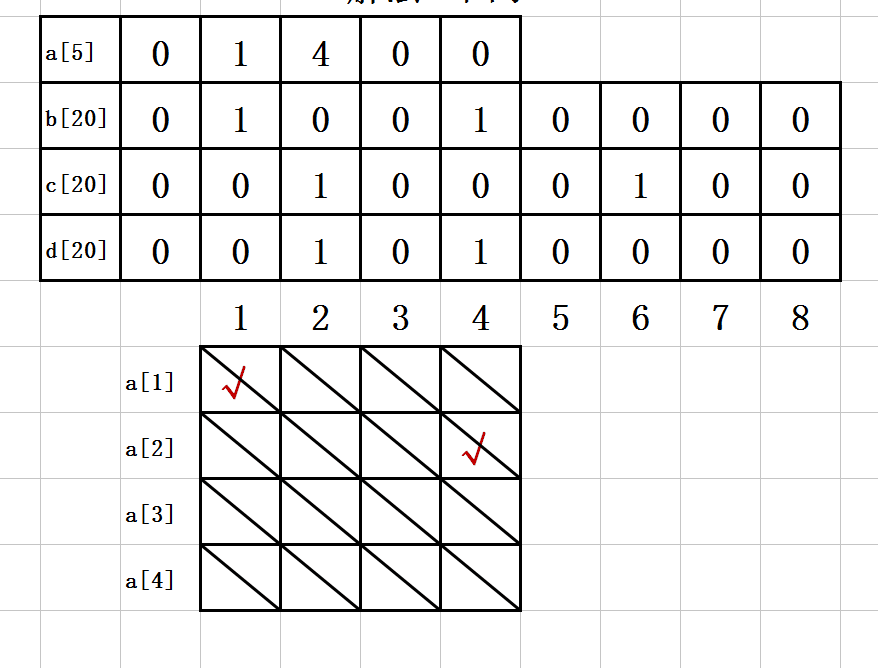
4. 第三步:
a[1]=1;
b[1]=1;
c[2]=1;
d[4]=1;
a[2]=4;
b[4]=1;
c[6]=1;
d[2]=1;
如图示:
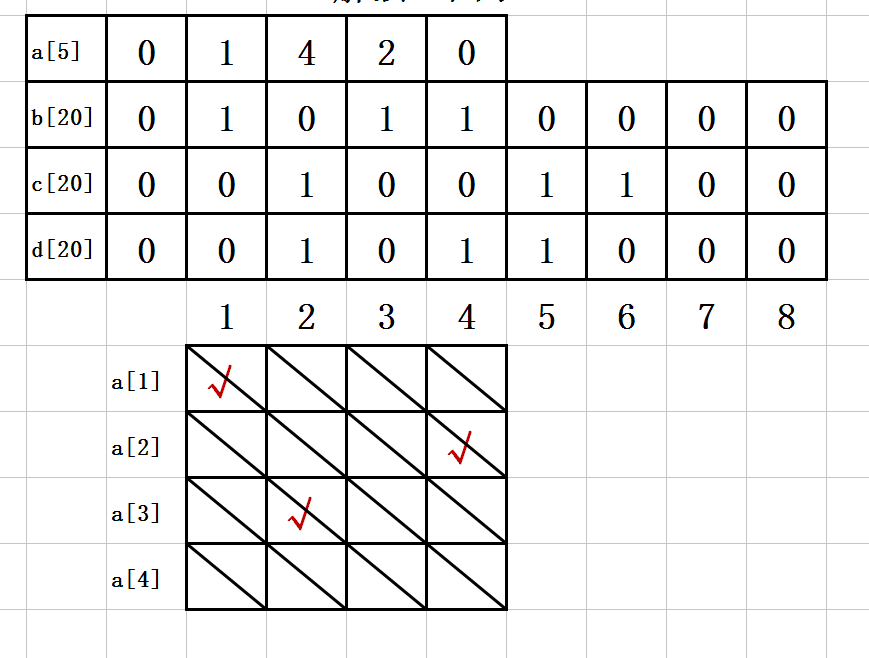
5. 第四步:
a[1]=1;
b[1]=1;
c[2]=1;
d[4]=1;
a[2]=4;
b[4]=1;
c[6]=1;
d[2]=1;
a[3]=2;
b[3]=1;
c[5]=1;
d[5]=1;
如图示:
6. 第五步:
重复上面的递归循环,每当发现某次循环结束但还是没找到正确位置时,回到上层循环(也就是上层皇后右移),然后继续往下递归判断,若上层循环也结束了仍不能找到一组正确的解,那就再回到上上层循环,以此类推,直到找到正确的一组解
7. 第N步:
a[1]=2;
a[2]=4;
a[3]=1;
a[4]=3;
b[1]=1;
b[2]=1;
b[3]=1;
b[4]=1;
c[3]=1;
c[4]=1;
c[6]=1;
c[7]=1;
d[2]=1;
d[3]=1;
d[5]=1;
d[6]=1;
如图示:
4、结果显示
5、参考文献:
算法设计与分析吕国英版(第三版) p210(8皇后问题)
6、附件
编者:阿沐
特别声明:该作品为博主原创,若发现哪里写的不对或者对哪部分不明白的请及时联系阿沐
阿沐QQ543206554
Loading...







 微信扫一扫,打赏阿沐吧~
微信扫一扫,打赏阿沐吧~


评论