回溯算法解决8皇后问题
编者:16计外1班 阿沐 指导老师:李老师
1、问题描述:
8皇后问题:要在8*8的国际象棋棋盘中放8个皇后,使任意两个皇后都不能互相吃掉。规则是皇后能吃掉同一行、同一列、同一对角线的任意棋子。图1-1为一种方案,求所有的解。
2、模型建立
设8个皇后为Xi,她们分别在第i行(i=1,2,3,4,5,6,7,8),这样问题的解的空间,就是一个8个皇后所在列的序列,为n元一维向量(X1,X2,X3,X4,X5,X6,X7,X8),搜索空间是1<=Xi<=8(i=1,2,3,4,5,6,7,8),共88个状态。约束条件是8个点(1,X1)、(2,X2)、(3,X3)、(4,X4)、(5,X5)、(6,X6)、(7,X7)、(8,X8)不在同一列和同一对角线上。
3、算法设计
回溯算法
回溯算法的基本思想是:从一条路往前走,能进则进,不能进则退回来,换一条路再试。在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。当探索到某一结点时,要先判断该结点是否包含问题的解,如果包含,就从该结点出发继续探索下去,如果该结点不包含问题的解,则逐层向其祖先结点回溯。
加约束条件的枚举算法:
最简单的算法就是通过八重循环模拟搜索空间中的88个状态,按深度优先思想,从第一个皇后开始搜索,确定一个位置后,再搜索第二个皇后的位置;......;每前进一步检查是否满足约束条件,不满足时用continue语句回溯到上一个皇后,继续尝试下一个位置;满足约束条件时,开始搜索下一个皇后的位置,直到找出问题的解。
约束条件有3个:
1. 不在同一列的表达式为:Xi≠Xj;
2. 不在同一主对角线上的表达式为:Xi-i≠Xj-j;
3. 不在同一负对角线上的表达式为:Xi+i≠Xj+j。
条件2和3可以合并为一个“不在同一对角线上”的约束条件,表示为:
abs(Xi-Xj)≠abs(i-j) abs()取绝对值。
4、代码实现(Java)
package gxr;
public class Queen {
public static void main(String[] args) {
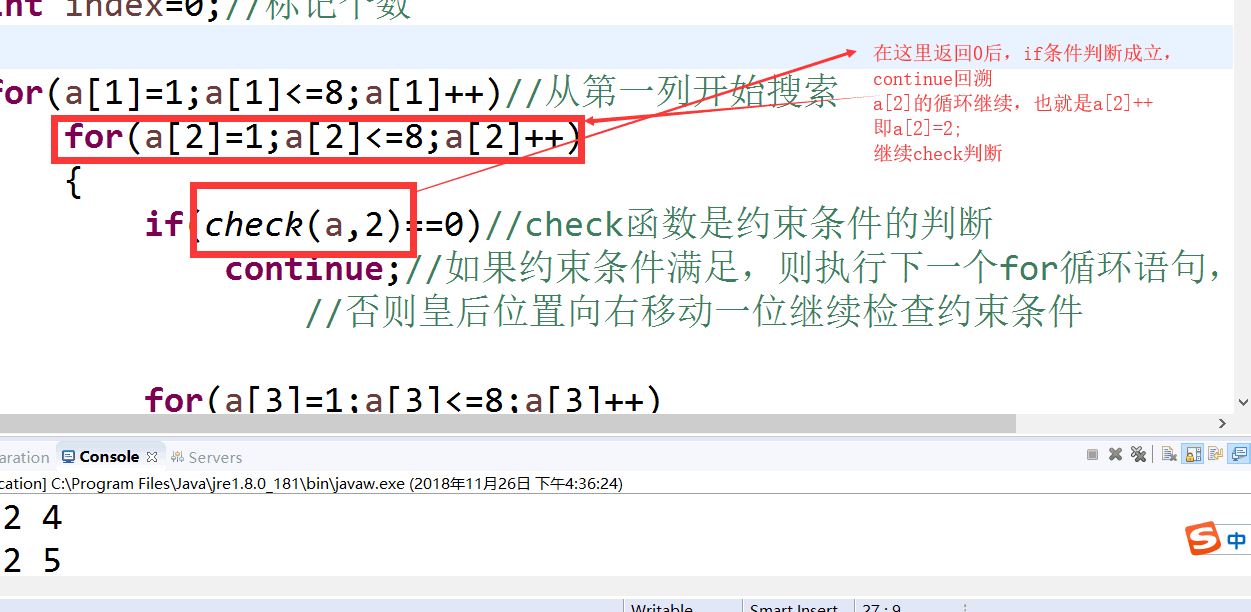
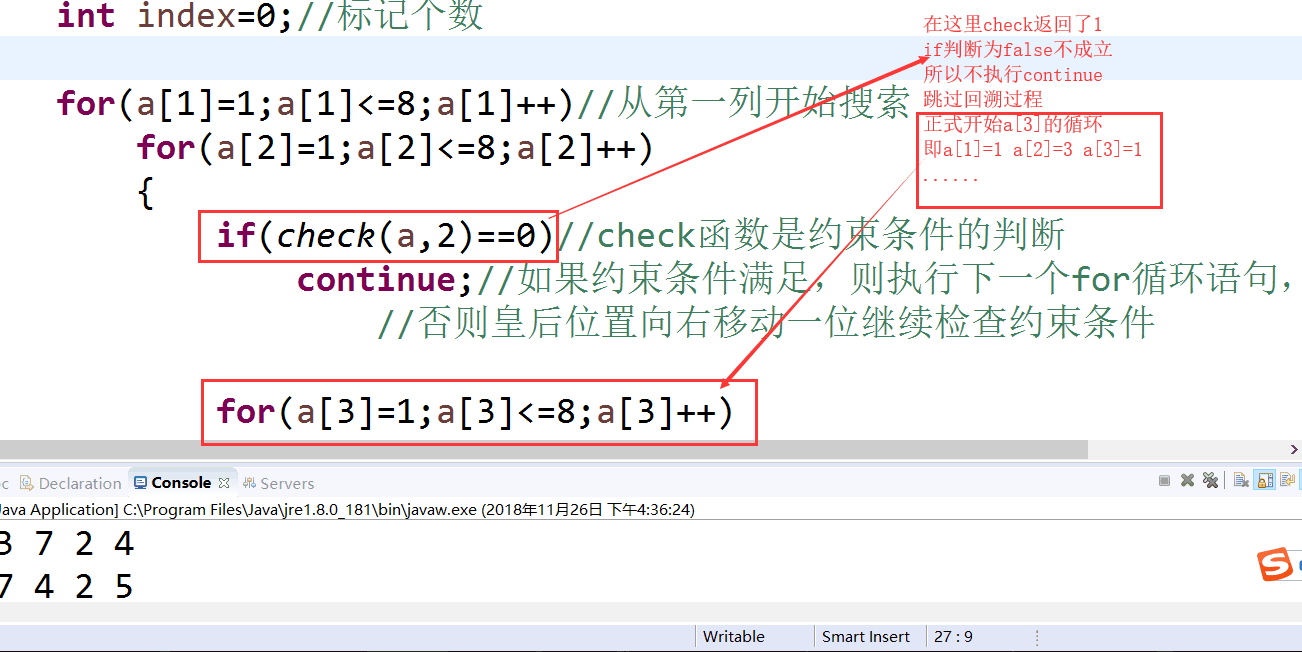
int[] a=new int[9];//初始化定义数组
int index=0;//标记个数
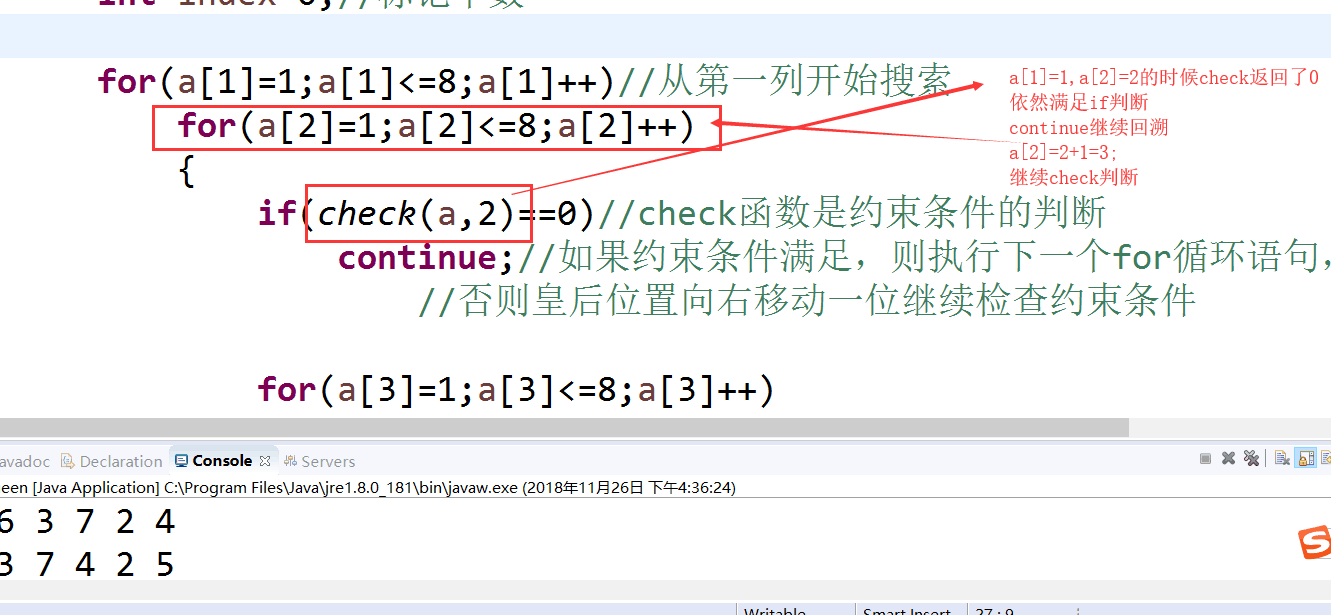
for(a[1]=1;a[1]<=8;a[1]++)//从第一列开始搜索
for(a[2]=1;a[2]<=8;a[2]++)
{
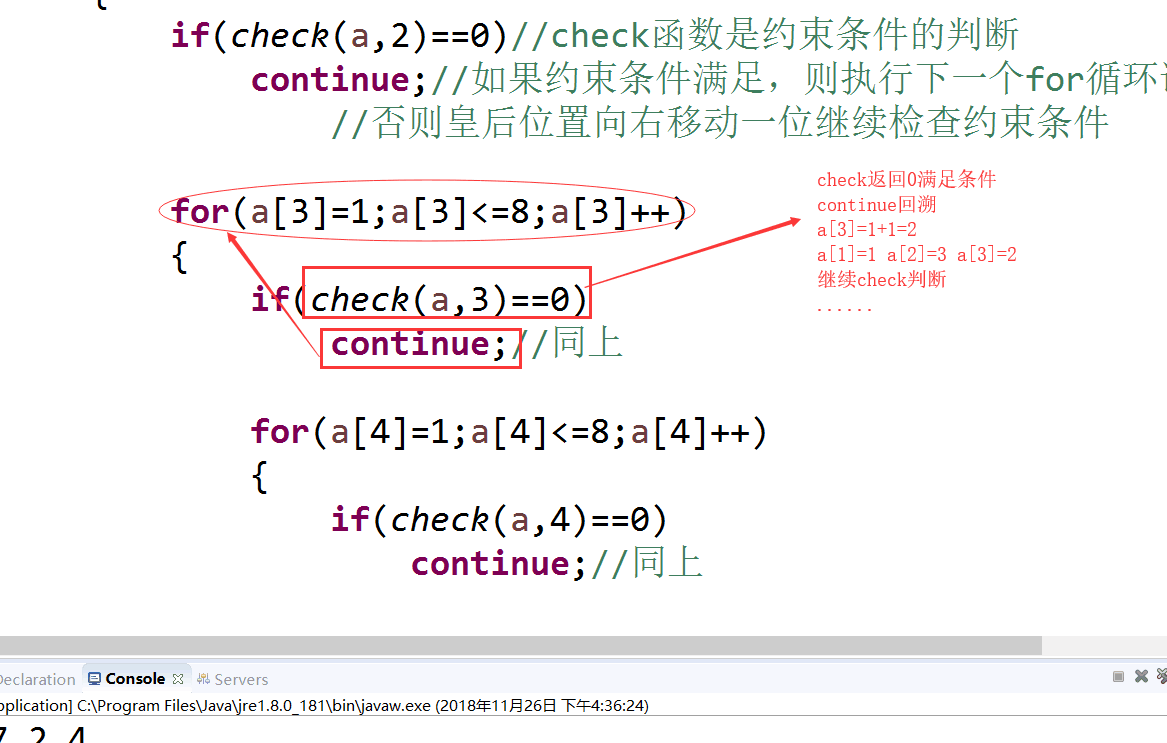
if(check(a,2)==0)//check函数是约束条件的判断
continue;//如果约束条件满足,则执行下一个for循环语句,
//否则皇后位置向右移动一位继续检查约束条件
for(a[3]=1;a[3]<=8;a[3]++)
{
if(check(a,3)==0)
continue;//同上
for(a[4]=1;a[4]<=8;a[4]++)
{
if(check(a,4)==0)
continue;//同上
for(a[5]=1;a[5]<=8;a[5]++)
{
if(check(a,5)==0)
continue;//同上
for(a[6]=1;a[6]<=8;a[6]++)
{
if(check(a,6)==0)
continue;//同上
for(a[7]=1;a[7]<=8;a[7]++)
{
if(check(a,7)==0)
continue;//同上
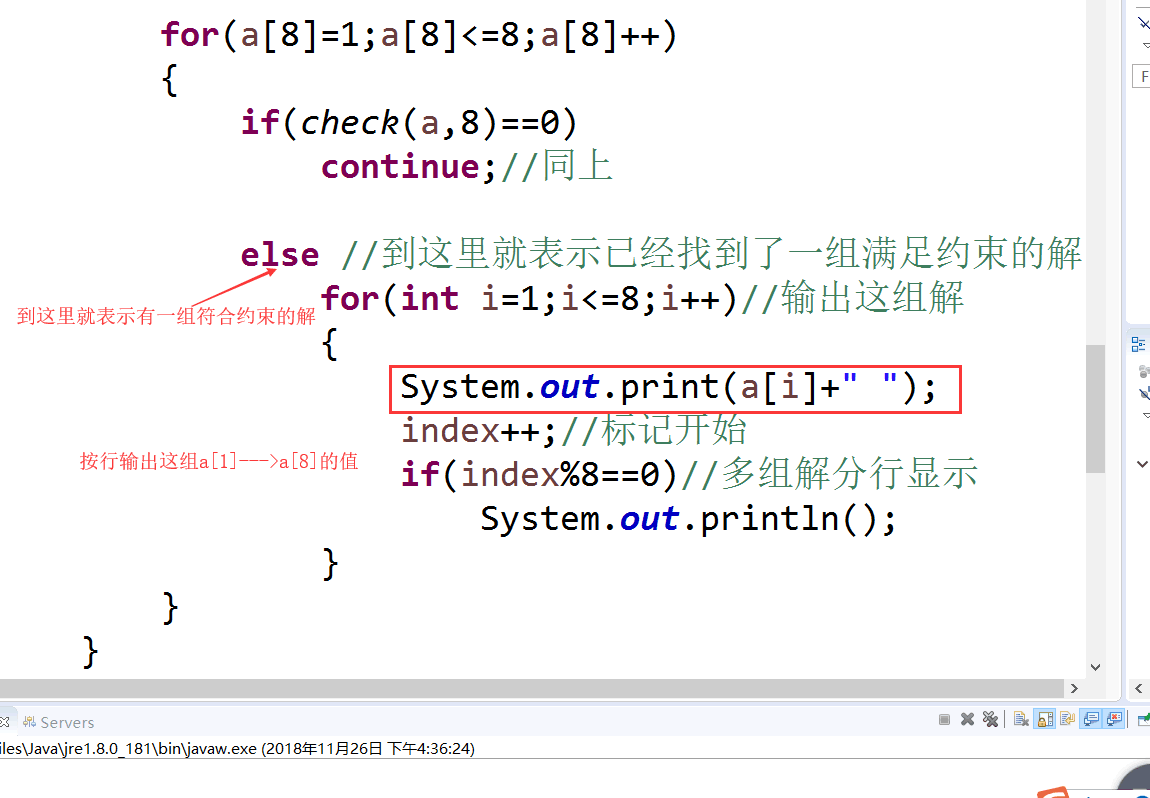
for(a[8]=1;a[8]<=8;a[8]++)
{
if(check(a,8)==0)
continue;//同上
else //到这里就表示已经找到了一组满足约束的解
for(int i=1;i<=8;i++)//输出这组解
{
System.out.print(a[i]+" ");
index++;//标记开始
if(index%8==0)//多组解分行显示
System.out.println();
}
}
}
}
}
}
}
}
System.out.println(index/8);//输出满足约束解的个数
}
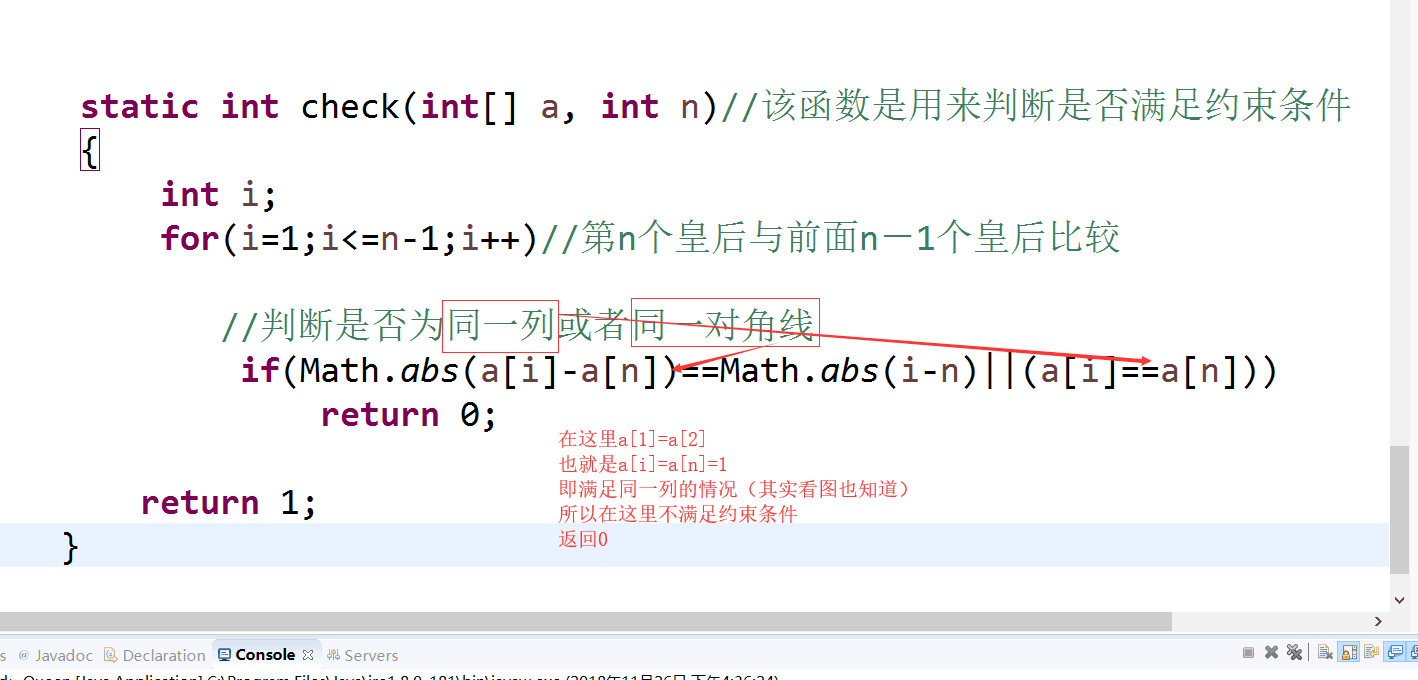
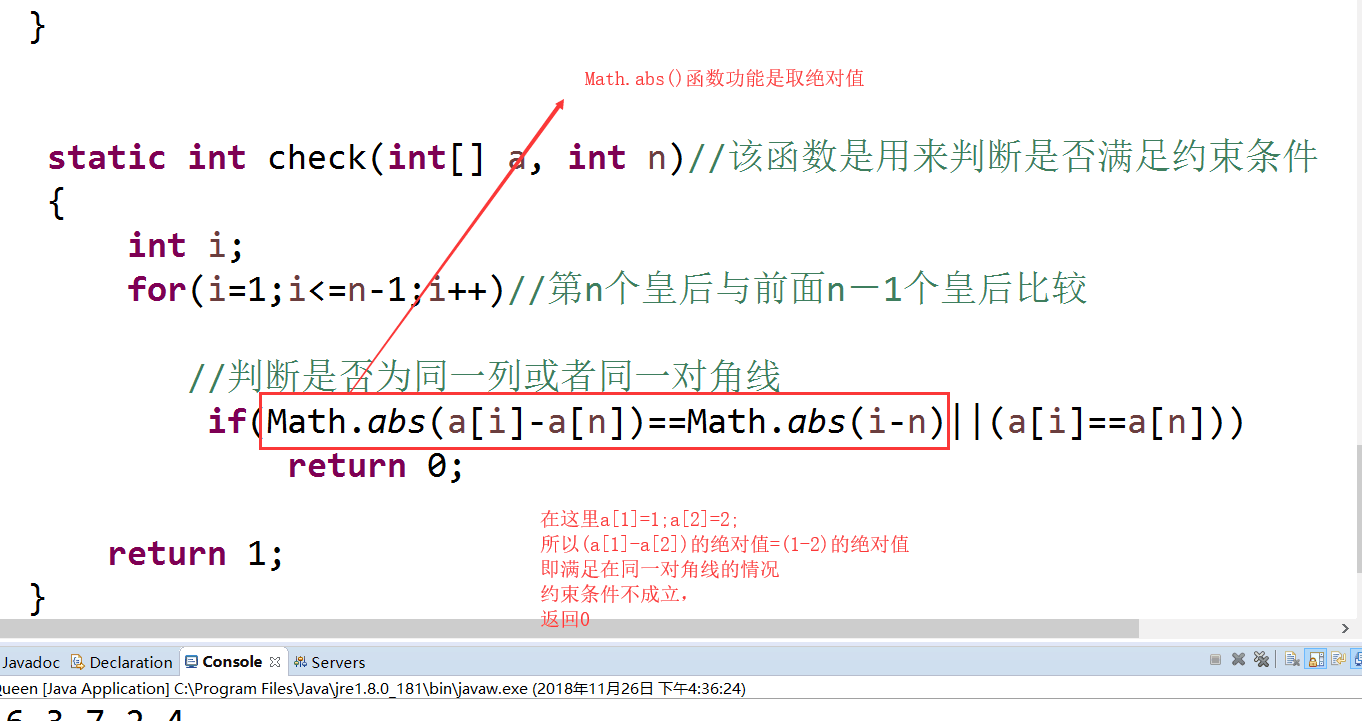
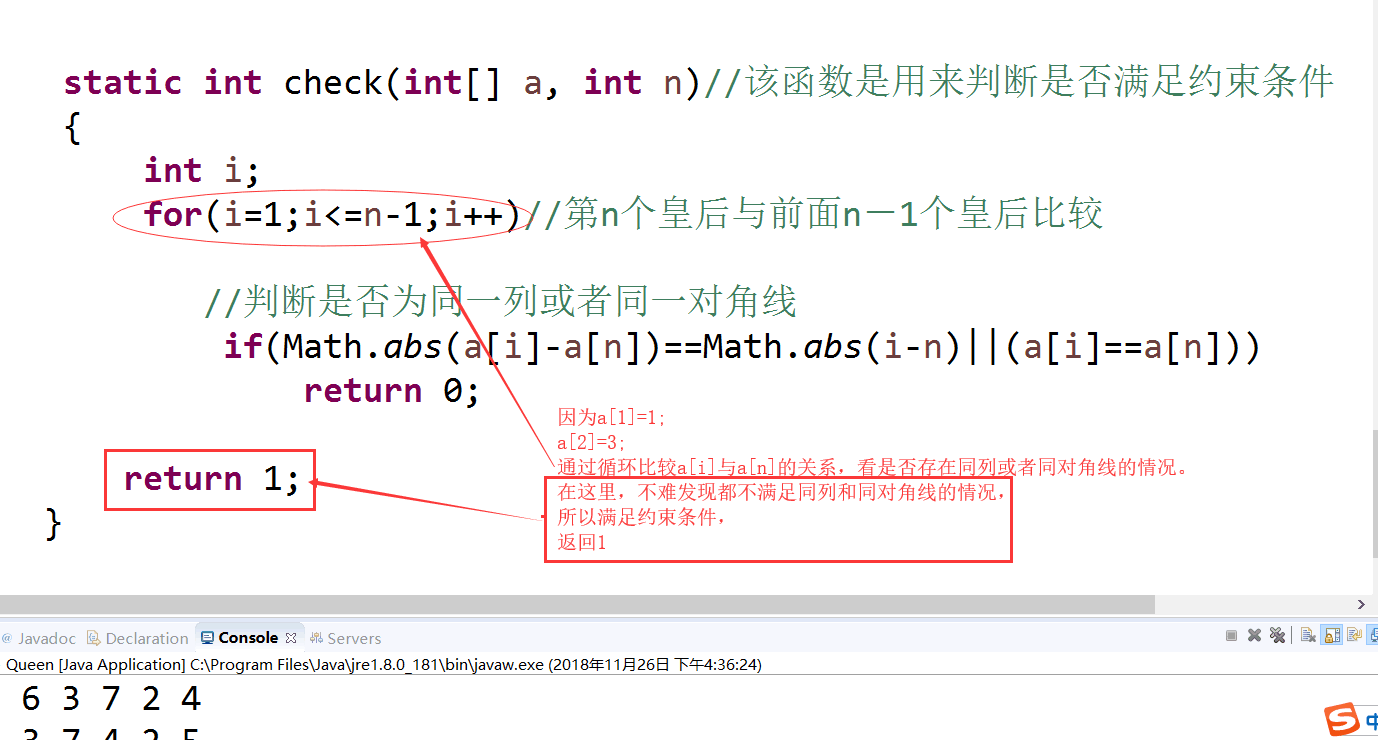
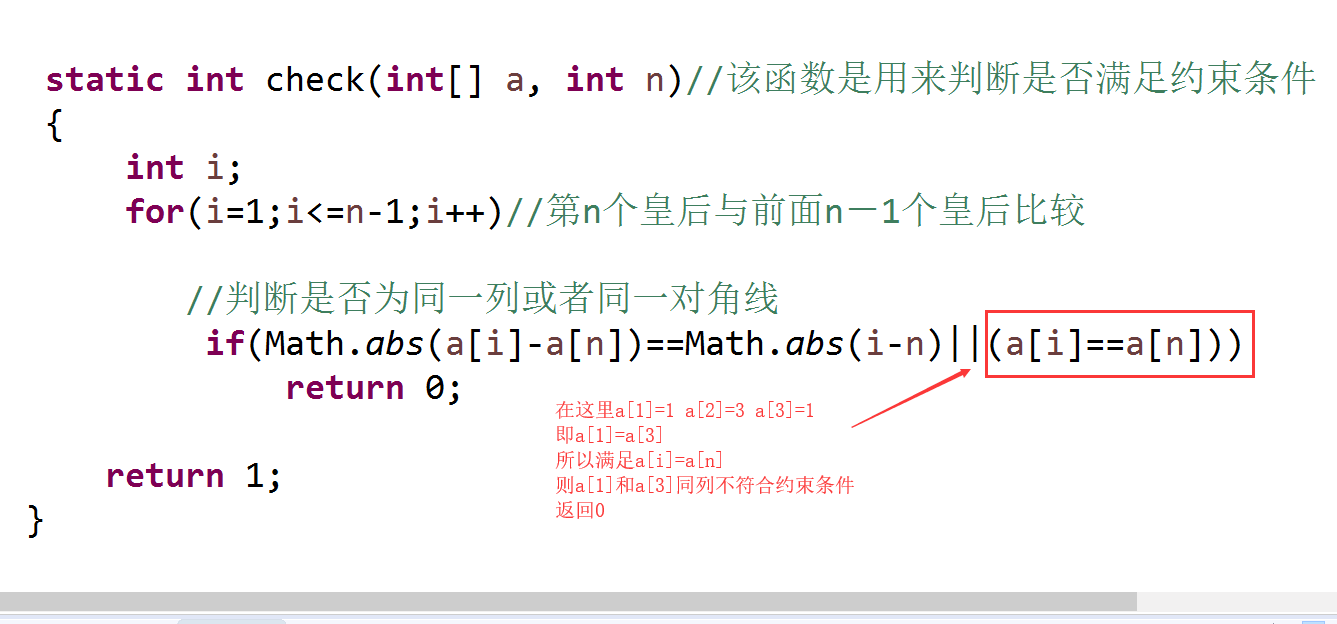
static int check(int[] a, int n)//该函数是用来判断是否满足约束条件
{
int i;
for(i=1;i<=n-1;i++)//第n个皇后与前面n-1个皇后比较
//判断是否为同一列或者同一对角线
if(Math.abs(a[i]-a[n])==Math.abs(i-n)||(a[i]==a[n]))
return 0;
return 1;
}
}
5、推演过程
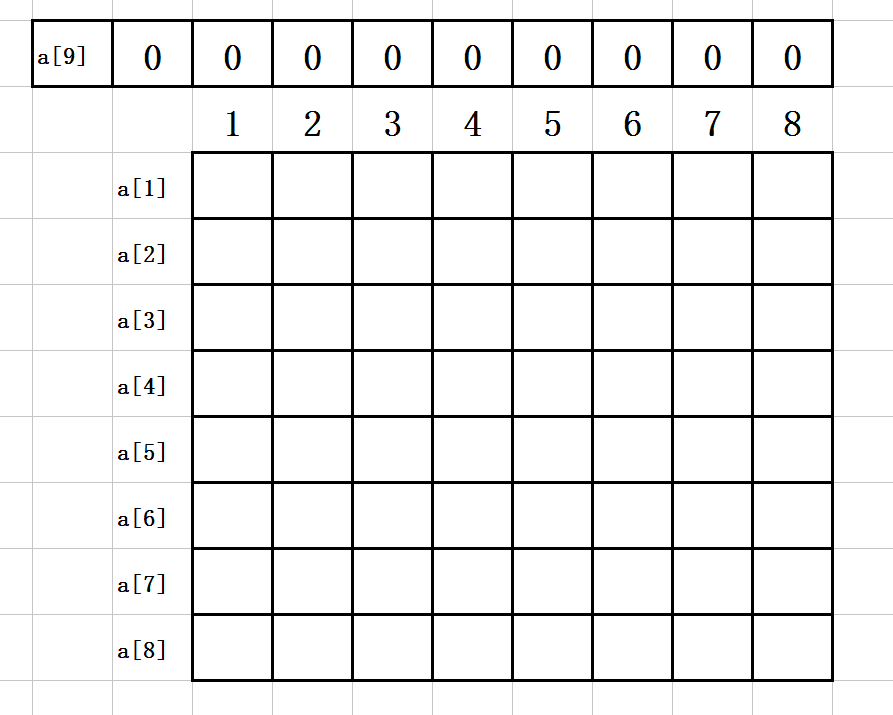
1. 初始图如下:
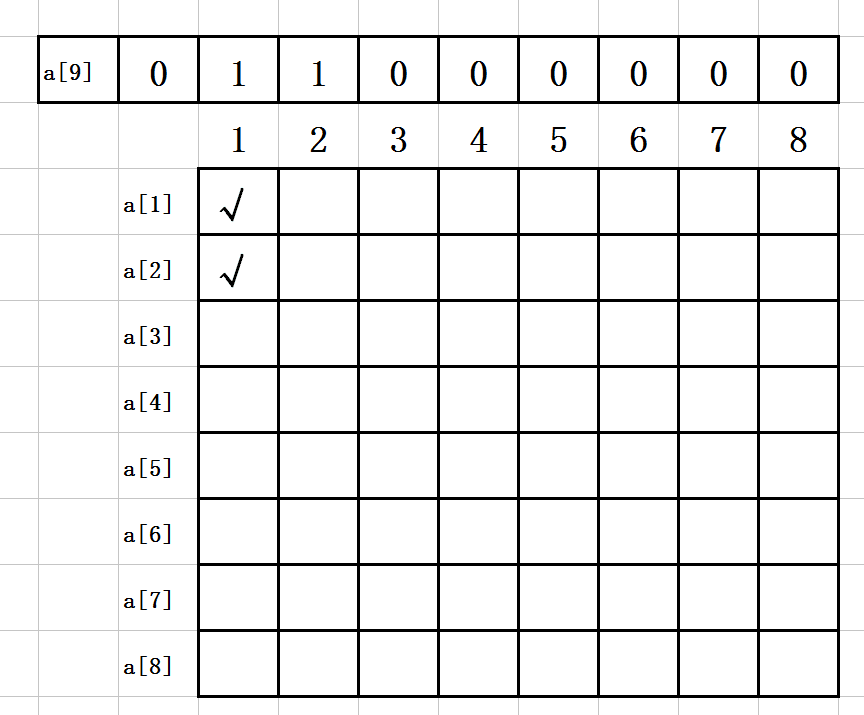
2. 第一步:
a[1]=1;
a[2]=1;
如图示:
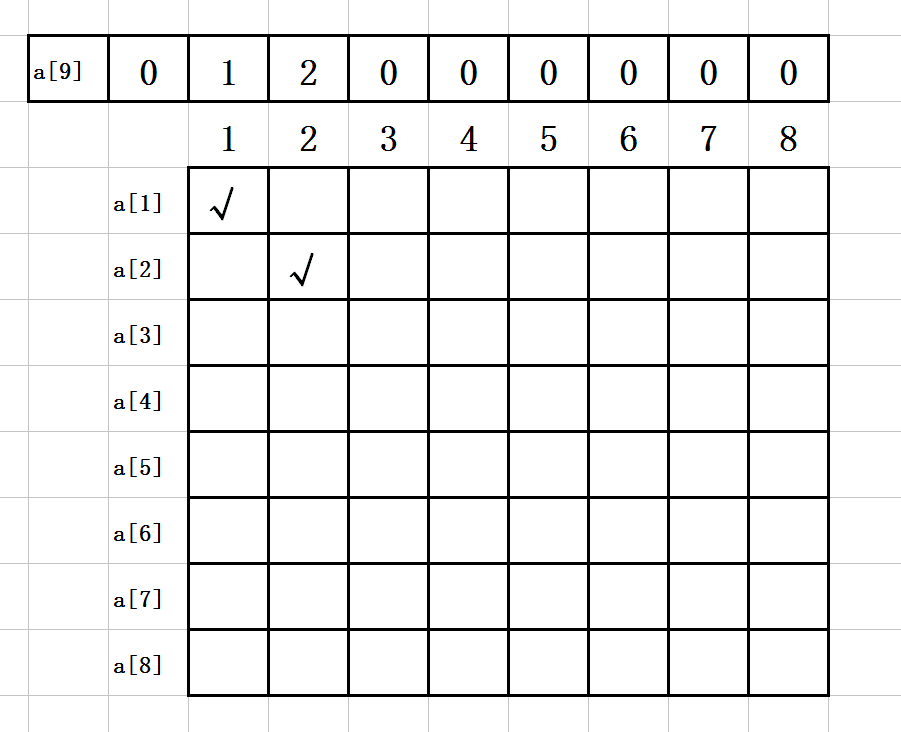
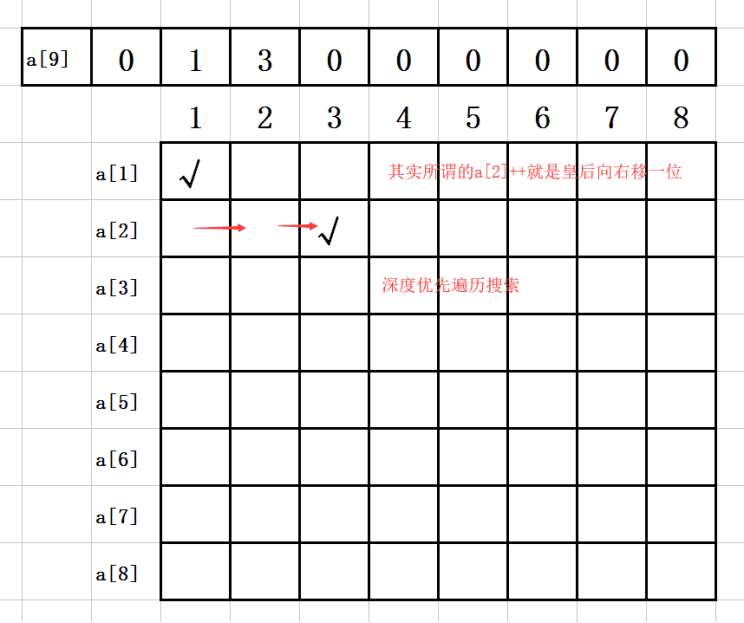
3. 第二步:
a[1]=1;
a[2]=2;
如图示:
4. 第三步:
a[1]=1;
a[2]=3;
如图示:
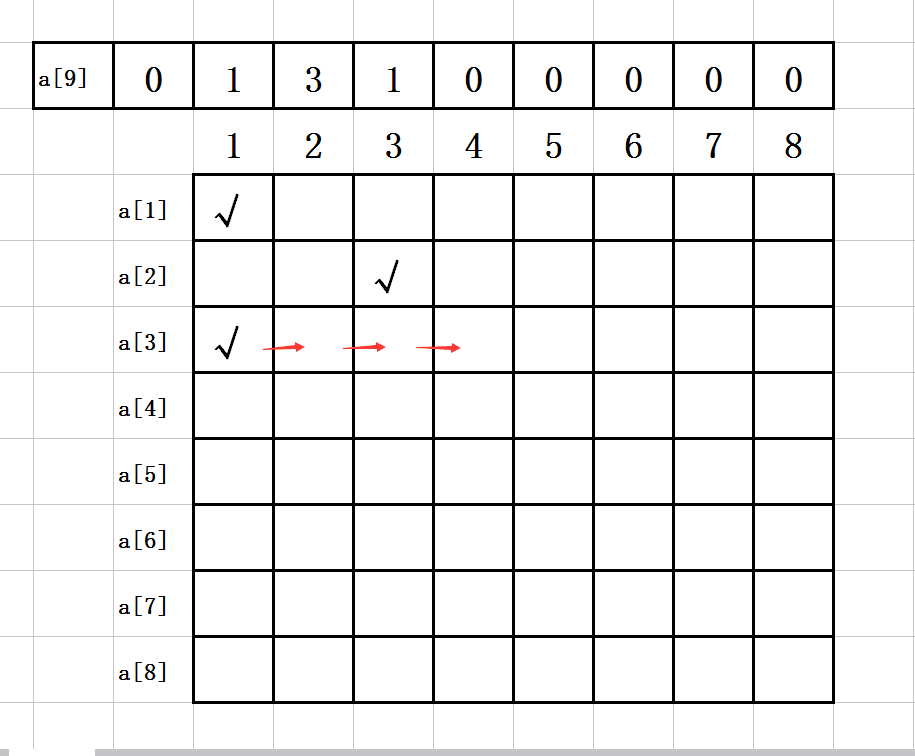
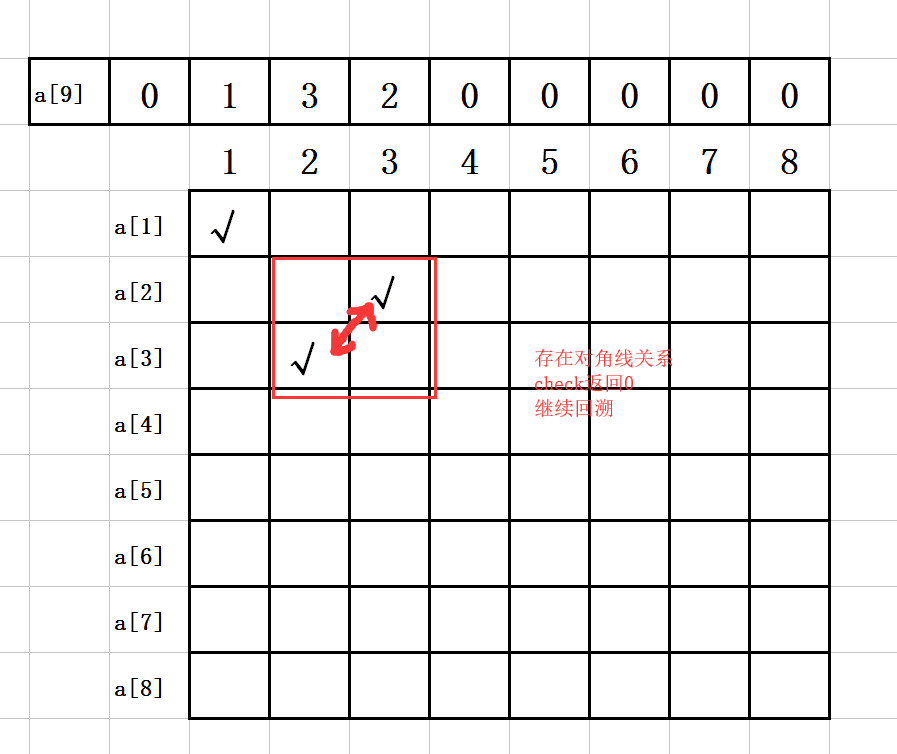
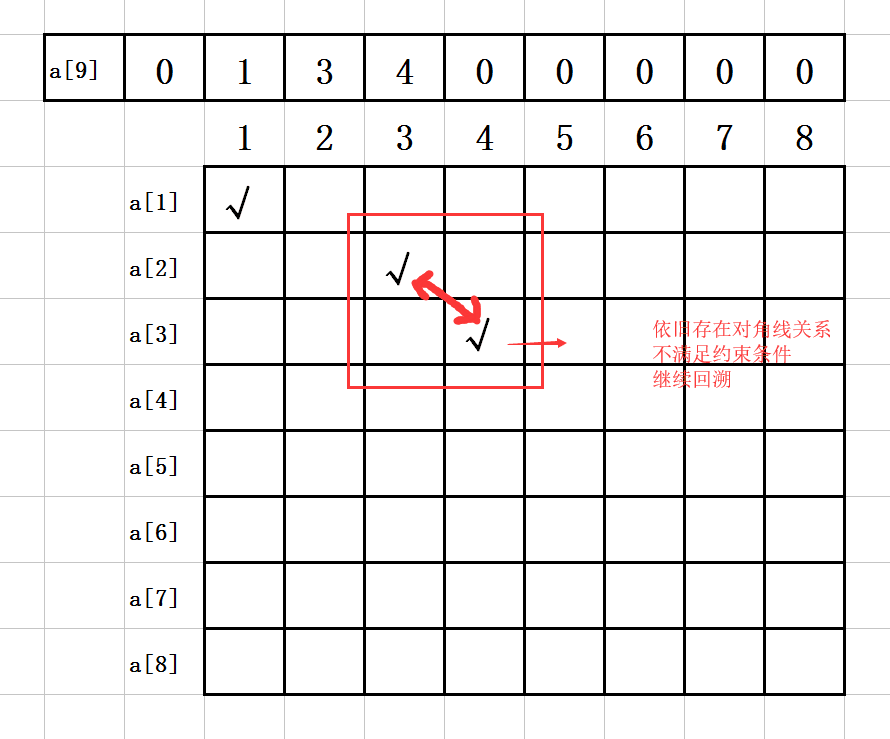
5. 第四步:
a[1]=1;
a[2]=3;
a[3]=1;
如图示:
6. 第五步:
a[1]=1;
a[2]=3;
a[3]=2;
如图示:
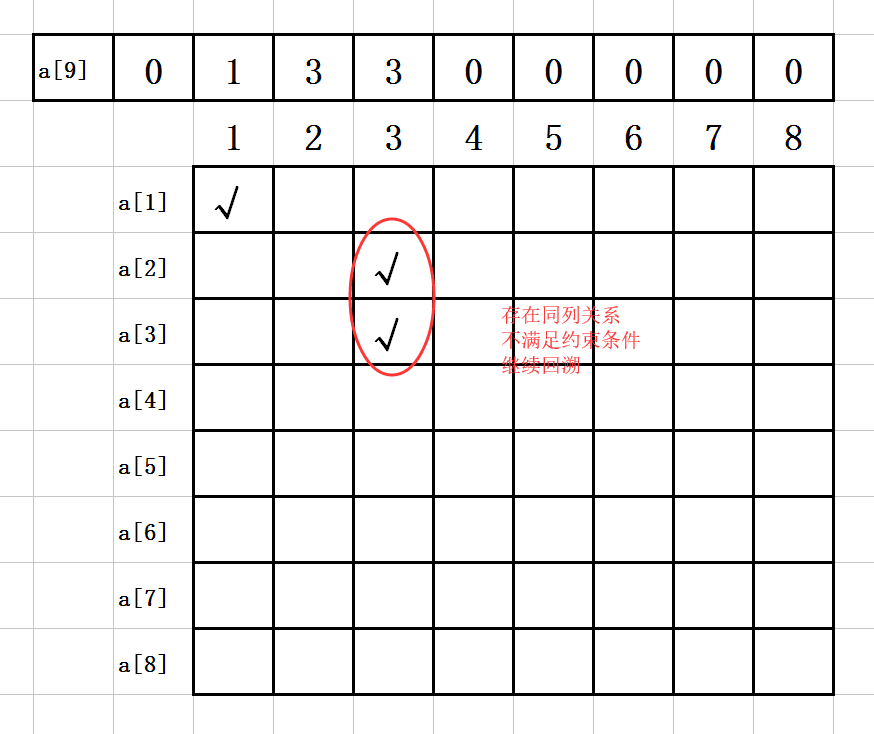
7. 第六步:
a[1]=1;
a[2]=3;
a[3]=3;
如图示:
8. 第七步:
a[1]=1;
a[2]=3;
a[3]=4;
如图示:
9. 第八步:
a[1]=1;
a[2]=3;
a[3]=5;
如图示:
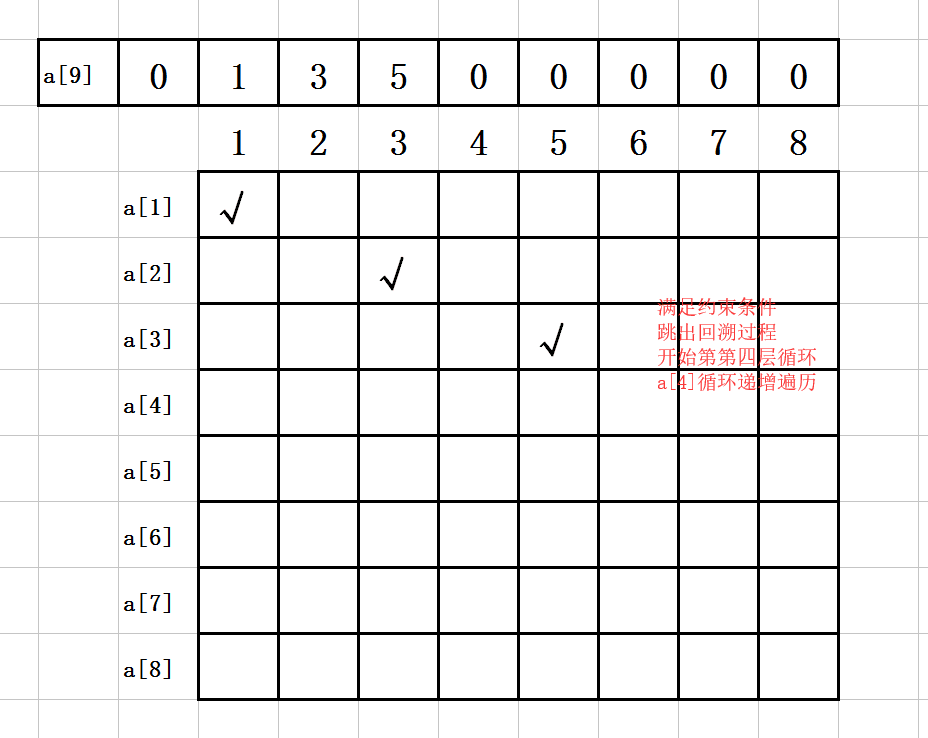
10. 第九步:
a[1]=1;
a[2]=3;
a[3]=5;
a[4]=1;
如图示:
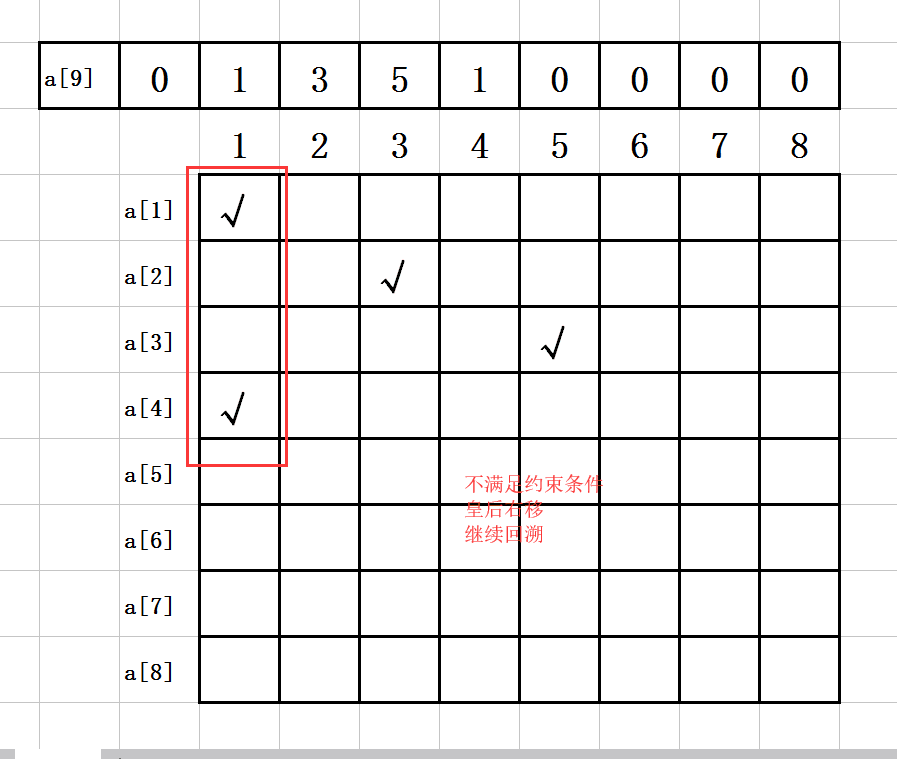
11. 第十步:
a[1]=1;
a[2]=3;
a[3]=5;
a[4]=2;
如图示:
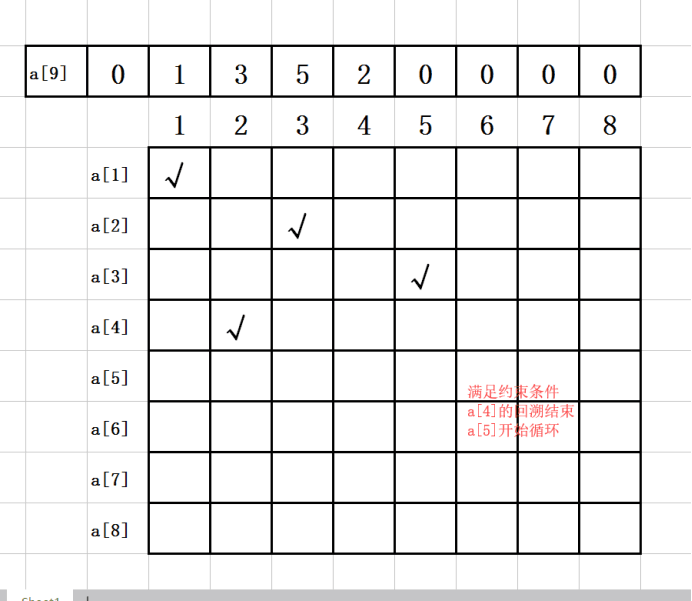
12. 第十一步:
a[1]=1;
a[2]=3;
a[3]=5;
a[4]=2;
a[5]=1;
如图示:
13. 第十二步:
重复前面判断回溯过程,确定a数组的全部值
在这里要重点提到的是:
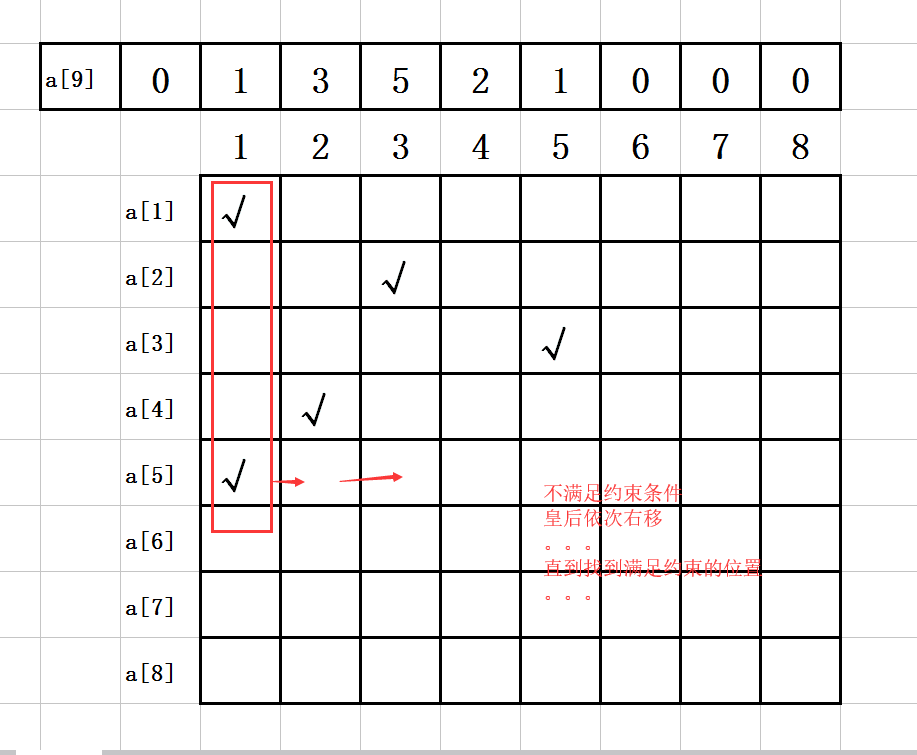
按照之前的步骤走下去可能会出现后面一直存在不满足约束条件的情况,这个时候就要跳回上一级,上一级的皇后后移一位继续判断回溯,如果还不行,继续跳到上上级,上上级皇后后移一位继续判断回溯......这样就能得到满足约束的解。
14. 第n步:
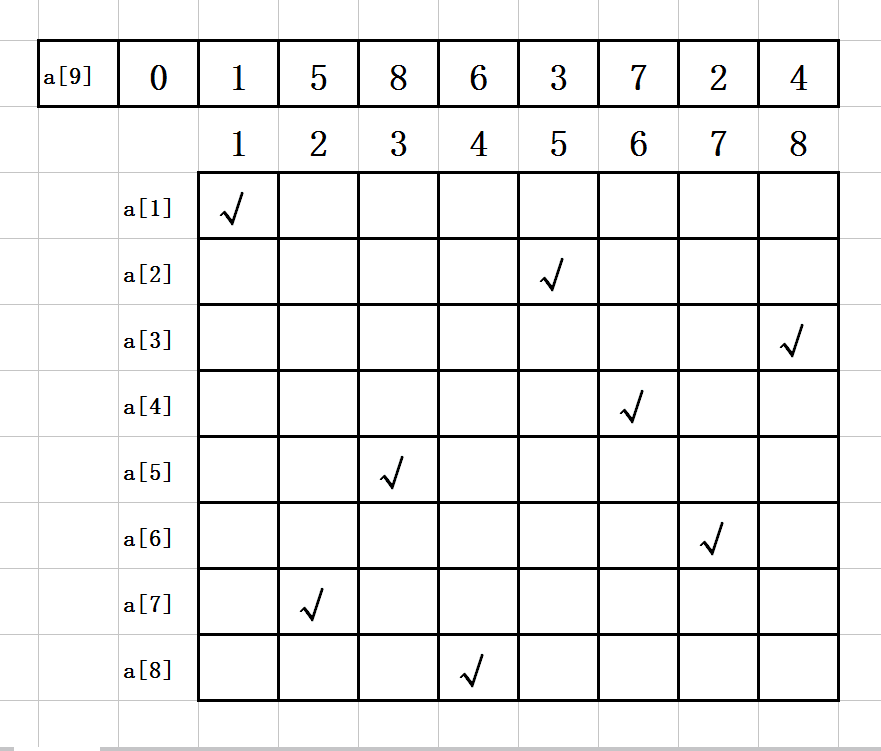
找到第一组符合约束条件的值
a[1]=1;
a[2]=5;
a[3]=8;
a[4]=6;
a[5]=3;
a[6]=7;
a[7]=2;
a[8]=4;
如图示:
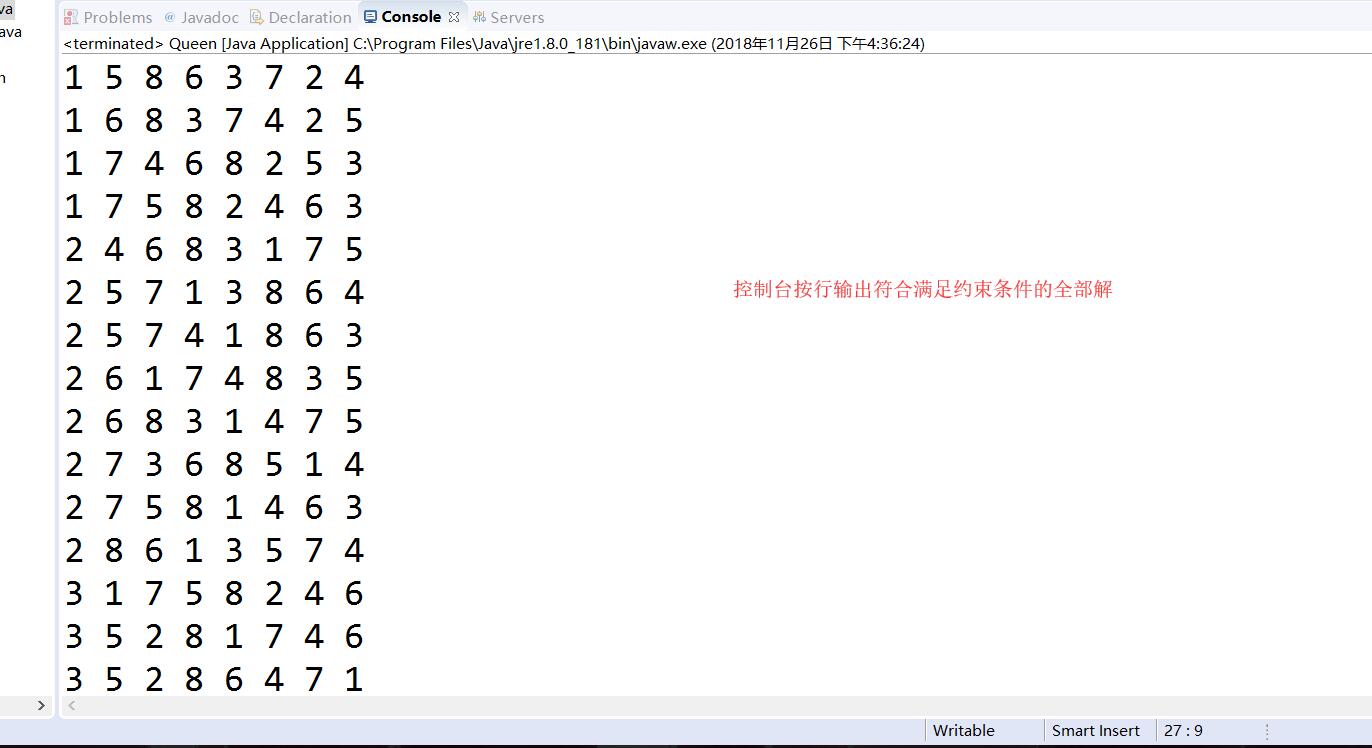
6、结果显示
控制台显示:
7、参考文献:
算法设计与分析吕国英版(第三版) p207(8皇后问题)
8、附件
编者:阿沐
特别声明:该作品为博主原创,若发现哪里写的不对或者对哪部分不明白的请及时联系阿沐
阿沐QQ543206554
Loading...




 微信扫一扫,打赏阿沐吧~
微信扫一扫,打赏阿沐吧~


评论
访客
回复牛批 牛批!