简单的聚类入门篇

阿沐学习日记 2019-03-27 720 1

简单的聚类入门篇

刚学python，为了让我们更快地入门新语言，老师特意出了下面这个题目：

一、问题解析：

题目的大概意思就是：

1、随机生成很多点

2、自己确定几个中心点

3、然后把这些点分类

4、分类的标准是按离中心点的距离

说白了，就是自己设置中心点，然后把中心点旁边的一些点作为一块这样分类，有几个中心点就可以分成几块

二、解题思路：

根据题意，基本确定这里的算法就是算距离了，而且是两个点的距离计算。

在python里math模块里直接封装了一个hypot()的方法，hypot()方法返回的欧几里德范数 sqrt(x*x + y*y)这就是两个点的距离计算公式。

在分类的时候为了更好的显示效果，下面就对分好的不同类进行不同颜色的显示以作区别。

三、算法实现：

1、基于最简单的象限区分法：

①算法简介：

a、在绘制画布时确定画布大小（countX * countY）

b、根据画布大小确定四个象限（区分节点 countX/2 、countY/2）

c、随机生成数组x和y，(x[i],y[i])作为第i个随机生成点的坐标

d、循环遍历所有点，分别判断点所在象限

e、位于不同象限的点显示不同颜色

②代码实现（python）：

import matplotlib.pyplot as plt
import random
import math
a = range(0,1000,1)
x = random.sample(a, 1000)
y = random.sample(a, 1000)
countX=len(x)
countY=len(y)
print(x)
print(y)

#循环遍历所有点，分别判断点所在象限,位于不同象限的点显示不同颜色
for i in range(0,countX) :
    if x[i]<=countX/2 :
        if y[i]<=countY/2:
            plt.scatter(x[i], y[i], color='m')
        else:
            plt.scatter(x[i], y[i], color='g')
    if x[i]>=countX/2 :
        if y[i]<=countY/2 :
            plt.scatter(x[i], y[i], color='r')
        else :
            plt.scatter(x[i], y[i], color='b')


plt.show()

③效果显示（这里是1000个随机点的显示效果）：

④补充说明：这里分象限其实就是算距离的另一种体现，只不过是把中心点确定为每个象限的矩形中心点，块状聚类分布！

2、基于一般的距离中心点区分法：

①算法简介：

a、在绘制画布时确定画布大小（countX * countY）

b、根据画布大小确定四个中心点（区分节点 countX * 1/4 、countX * 3/4、countY * 1/4 、countY * 3/4）

c、随机生成数组x和y，(x[i],y[i])作为第i个随机生成点的坐标

d、循环遍历所有点，分别计算到各个中心点的距离，若距离小于countX * 1/4 则可作为一类划分（这里可以看成有4个分别以中心点为圆心、半径为countX * 1/4 的圆，若其他点在某个圆的范围内即可划分为一类）

e、位于不同类别的点显示不同颜色

②代码实现（python）：

import matplotlib.pyplot as plt
import random
import math
a = range(0,1000,1)
x = random.sample(a, 1000)
y = random.sample(a, 1000)
countX=len(x)
countY=len(y)
minX=countX*0.25
minY=countY*0.25
maxX=countX*0.75
maxY=countY*0.75
print(x)
print(y)

plt.scatter(x,y,color = 'k')

#循环遍历所有点，分别计算到各个中心点的距离，若距离小于countX * 1/4 则可作为一类划分
# （这里可以看成有4个分别以中心点为圆心、半径为countX * 1/4 的圆，若其他点在某个圆的范围内即可划分为一类）
for i in range(0,len(x)):
    if math.hypot(x[i]-minX,y[i]-minY)<= minX:
        plt.scatter(x[i], y[i], color='m')
    if math.hypot(x[i]-minX, y[i]-maxY) <=minX :
        plt.scatter(x[i], y[i], color='g')
    if math.hypot(x[i] - maxX, y[i] - minY) <= minX:
        plt.scatter(x[i], y[i], color='r')
    if math.hypot(x[i] - maxX, y[i] - maxY) <= minX:
        plt.scatter(x[i], y[i], color='b')

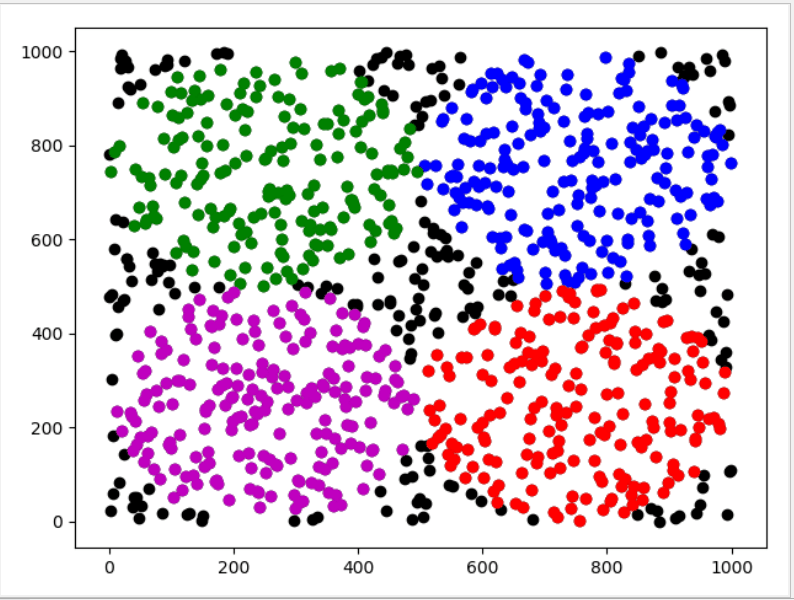
plt.show()

③效果显示（这里是1000个随机点的显示效果）：

④补充说明：由上图可知，根据与四个中心点距离计算判断，所划分的四个不同区域（四种非黑色点区域）都呈现圆形分布，而画布边角以及中心的那些黑色点区域并未划分是因为他们到最近的中心点的距离大于半径，也就是在四个圆区域外，所以不予划分。虽然这种算法在设计上可能不算很好，但着实是一种聚类的思想体现。

3、基于算法二的可控实现：（这里指定划分三个类别）

①算法简介：

a、随机生成数组x和y，(x[i],y[i])作为第i个随机生成点的坐标

b、参考画布大小，自定义输入三个中心点的坐标

c、循环遍历所有点，分别计算每个点到各个中心点的距离，保存在一个list里

d、通过list找出最小值，也就是确定离某个中心点距离最小的值

e、通过判断距离最小值确定类别，位于不同类别的点显示不同颜色

②代码实现（python）：

import matplotlib.pyplot as plt
import math
import random

a=range(0,1000,1)
x=random.sample(a,1000)
y=random.sample(a,1000)

print(x)
print(y)
#输入三个中心点
x1 = input("请输入第一个中心点的横坐标:")
y1 = input("请输入第一个中心点的纵坐标:")
x2 = input("请输入第二个中心点的横坐标:")
y2 = input("请输入第二个中心点的纵坐标:")
x3 = input("请输入第三个中心点的横坐标:")
y3 = input("请输入第三个中心点的纵坐标:")

#分别计算每个点到三个中心点的距离
for i in range(0,len(x)):
    s1 = math.hypot(x[i] - int(x1), y[i] - int(y1))
    s2 = math.hypot(x[i] - int(x2), y[i] - int(y2))
    s3 = math.hypot(x[i] - int(x3), y[i] - int(y3))
    s=[]
    s.append(s1)
    s.append(s2)
    s.append(s3)

    min=s[0]
    for j in range(1,len(s)):
        if s[j]<=min :
            min=s[j]
    if min == s1:
        plt.scatter(x[i], y[i], color='m')
    if min == s2:
        plt.scatter(x[i], y[i], color='g')
    if min == s3:
        plt.scatter(x[i], y[i], color='r')

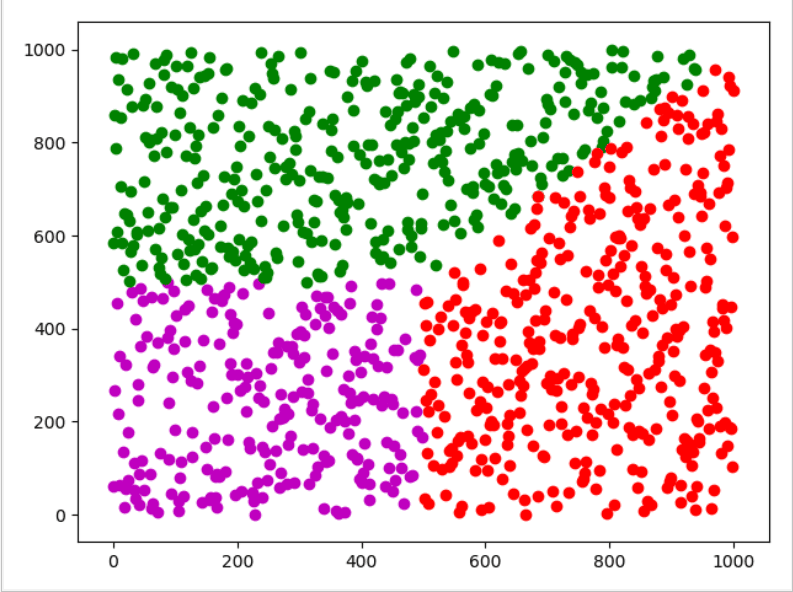
plt.show()

③效果显示（这里是1000个随机点的显示效果）：