C语言编程：把一个分数分解成n个埃及分数的和形式，n最小

阿沐网上学习 2019-01-05 787 0 算法学习

C语言编程：把一个分数分解成n个埃及分数的和形式，n最小

1.题目分析：

把真分数表示为埃及分数之和的形式，所谓的埃及分数是指分子为1的分数

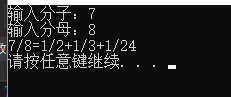
例如：7/8=1/2+1/3+1/24；要求用最少的埃及分数来表示

解析：设a、b为互质正整数，a<b 分数a/b 可用以下的步骤分解成若干个单位分数之和：

步骤一：用b 除以a，得商数q1 及余数r1。（r1=b - a*q1）

步骤二：把a/b 记作：a/b=1/(q1+1）+(a-r)/b(q1+1）

步骤三：重复步骤2，直到分解完毕

以上其实是数学家斐波那契提出的一种求解埃及分数的贪心算法，准确的算法表述应该是这样的：

设某个真分数的分子为a，分母为b;

把b除以a的商部分加1后的值作为埃及分数的某一个分母c；

将a乘以c再减去b，作为新的a；

将b乘以c，得到新的b；

如果a大于1且能整除b，则最后一个分母为b/a；算法结束；

或者，如果a等于1，则，最后一个分母为b；算法结束；

否则重复上面的步骤

2.C语言代码：

#include <stdlib.h>
#include <stdio.h>
 
int fun(int A, int B) 
{
	int b;//作为某个分数的分母
	int a;//B/A的商放a中
	int flag=0;//作为第一个分数输出的标志
 
	if (A == 1)			//当输入的分数的分子是1时直接输出
	{
		printf("%d/%d\n", A, B);
		return 0;
	}
	else
	{
		while (A!=1)
		{
 
		
		a = B / A;//商
		b = a + 1;
		if (flag == 0)
		{
			printf("1/%d", b);//第一个分数输出
			flag = 1;
		}
		else
		{
			printf("+1/%d", b);//非第一个分数输出
		}
		A = A * b - B;
		B = B * b;
		if (B%A == 0)
		{
			B = B / A;
			A = 1;
		}
		}
		printf("+%d/%d", A, B);
		
	}
	
	return 0;
}
 
int main()
{
	int A, B;
	printf("输入分子：");
	scanf_s("%d",&A);
	printf("输入分母：");
	scanf_s("%d", &B);
	printf("%d/%d=", A, B);
	fun(A, B);
	printf("\n");
	system("pause");
	return 0;
	
}